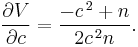Secretary problem
The secretary problem is one of many names for a famous problem of the optimal stopping theory. The problem has been studied extensively in the fields of applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem.
The basic form of the problem is the following. Imagine an administrator willing to hire the best secretary out of  rankable applicants for a position. The applicants are interviewed one-by-one in random order. A decision about each particular applicant is to be taken immediately after the interview. Once rejected, an applicant cannot be recalled. During the interview, the administrator can rank the applicant among all applicants interviewed so far, but is unaware of the quality of yet unseen applicants. The question is about the optimal strategy (stopping rule) to maximize the probability of selecting the best applicant.
rankable applicants for a position. The applicants are interviewed one-by-one in random order. A decision about each particular applicant is to be taken immediately after the interview. Once rejected, an applicant cannot be recalled. During the interview, the administrator can rank the applicant among all applicants interviewed so far, but is unaware of the quality of yet unseen applicants. The question is about the optimal strategy (stopping rule) to maximize the probability of selecting the best applicant.
The problem has a strikingly elegant solution. The optimal stopping rule prescribes to reject about 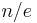 applicants after the interview (where e is the base of the natural logarithm) without choice then stop at the first applicant who is better than every applicant interviewed so far (or proceed to the last applicant if this never occurs). Sometimes this strategy is called the
applicants after the interview (where e is the base of the natural logarithm) without choice then stop at the first applicant who is better than every applicant interviewed so far (or proceed to the last applicant if this never occurs). Sometimes this strategy is called the 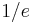 stopping rule, because the probability to stop at the best applicant with this strategy is about
stopping rule, because the probability to stop at the best applicant with this strategy is about 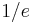 already for moderate values of
already for moderate values of  . One reason why the secretary problem has received so much attention is that the optimal policy for the problem (the stopping rule) is simple, and selects the single best candidate about 37% of the time, no matter for searching through 100 or 100,000,000 applicants. In fact, for every
. One reason why the secretary problem has received so much attention is that the optimal policy for the problem (the stopping rule) is simple, and selects the single best candidate about 37% of the time, no matter for searching through 100 or 100,000,000 applicants. In fact, for every  the probability of best choice with the optimal policy is at least
the probability of best choice with the optimal policy is at least 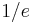 .
.
Because there are so many variations of the problem, the formulation will be re-stated once more:
- There is a single secretarial position to fill.
- There are n applicants for the position, and the value of n is known.
- The applicants, if seen altogether, can be ranked from best to worst unambiguously.
- The applicants are interviewed sequentially in random order, with each order being equally likely.
- Immediately after an interview, the interviewed applicant is either accepted or rejected, and the decision is irrevocable.
- The decision to accept or reject an applicant can be based only on the relative ranks of the applicants interviewed so far.
- The objective is to select the best applicant with the highest possible probability.
This is the same as maximizing the expected payoff, with payoff defined to be one for the best applicant and zero otherwise.
Terminology: A candidate is an applicant who, when interviewed, is better than all the applicants interviewed previously. Skip is used to mean "reject immediately after the interview".
Clearly, since the objective in the problem is to select the single best applicant, only candidates will be considered for acceptance. The "candidate" in this context corresponds to the concept of record in permutation.
Contents |
Deriving the optimal policy
The optimal policy for the problem is a stopping rule. Under it, the interviewer rejects the first r − 1 applicants (let applicant M be the best applicant among these r − 1 applicants), and then selects the first subsequent applicant that is better than applicant M. It can be shown that the optimal strategy lies in this class of strategies. For an arbitrary cutoff r, the probability that the best applicant is selected is
This sum is obtained by noting that if applicant i is the best applicant, then it is selected if and only if the best applicant among the first i − 1 applicants is among the first r − 1 applicants that were rejected. Letting n tend to infinity, writing  as the limit of r/n, using t for i/n and dt for 1/n, the sum can be approximated by the integral
as the limit of r/n, using t for i/n and dt for 1/n, the sum can be approximated by the integral
Taking the derivative of P(x) with respect to  , setting it to 0, and solving for x, we find that the optimal x is equal to 1/e. Thus, the optimal cutoff tends to n/e as n increases, and the best applicant is selected with probability 1/e.
, setting it to 0, and solving for x, we find that the optimal x is equal to 1/e. Thus, the optimal cutoff tends to n/e as n increases, and the best applicant is selected with probability 1/e.
For small values of n, the optimal r can also be obtained by standard dynamic programming methods. The optimal thresholds r and probability of selecting the best alternative P for several values of n are shown in the following table.
 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
 |
1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 |
 |
1.000 | 0.500 | 0.500 | 0.458 | 0.433 | 0.428 | 0.414 | 0.410 | 0.406 |
Note that the probability of selecting the best alternative in the classical secretary problem converges toward 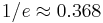 .
.
Alternative solution
This problem and several modifications can be solved (including the proof of optimality) in a straightforward manner by the Odds algorithm (2000) which also allows for other applications. Modifications for the secretary problem which can be solved by this algorithm include random availabilities of applicants, more general hypotheses for applicants to be of interest to the decision maker, group interviews for applicants, as well as certain models for a random number of applicants. None of these modifications are treated in this article.
Unknown number of applicants
A major drawback for applications of the solution of the classical secretary problem is that the number of applicants  must be known in advance. One way to overcome this problem is to suppose that the number of applicants is a random variable
must be known in advance. One way to overcome this problem is to suppose that the number of applicants is a random variable  with a known distribution of
with a known distribution of 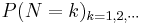 (Presman and Sonin, 1972). For this model, the optimal solution is in general much harder, however. Moreover, the optimal success probability is now no longer around 1/e. Indeed, it is intuitive that there should be a price to pay for not knowing the number of applicants. However, in this model the price is high. Depending on the choice of the distribution of
(Presman and Sonin, 1972). For this model, the optimal solution is in general much harder, however. Moreover, the optimal success probability is now no longer around 1/e. Indeed, it is intuitive that there should be a price to pay for not knowing the number of applicants. However, in this model the price is high. Depending on the choice of the distribution of  the optimal win probability is typically much lower than 1/e, and may even approach zero. This reduces the interest of this model for applications. Looking for ways to cope with this new problem led to the following approach and result:
the optimal win probability is typically much lower than 1/e, and may even approach zero. This reduces the interest of this model for applications. Looking for ways to cope with this new problem led to the following approach and result:
1/e-law of best choice
The essence of the model is based on the idea that real-world problems pose themselves in real time and that it is easier to estimate times in which specific events (arrivals of applicants) should occur more likely (if they do) than to estimate the distribution of the number of specific events which will occur. This idea lead to the following approach, the so-called Unified approach(1984):
The model: An applicant must be selected on some time interval ![[0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/b74093923941d33ee19becc5f4b48b25.png) from an unknown number
from an unknown number  of rankable applicants. The goal is to maximize the probability of selecting online the best under the hypothesis that all arrival orders of different ranks are equally likely. Suppose that all applicants have independently of each other the same arrival time density
of rankable applicants. The goal is to maximize the probability of selecting online the best under the hypothesis that all arrival orders of different ranks are equally likely. Suppose that all applicants have independently of each other the same arrival time density  on
on ![[0,T]](/2012-wikipedia_en_all_nopic_01_2012/I/b74093923941d33ee19becc5f4b48b25.png) and let
and let  denote the corresponding arrival time distribution function, that is
denote the corresponding arrival time distribution function, that is
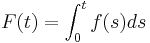 ,
, 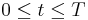 .
.
1/e-law: Let  be such that
be such that  Consider the strategy to wait and observe all applicants up to time
Consider the strategy to wait and observe all applicants up to time  and then to select, if possible, the first candidate after time
and then to select, if possible, the first candidate after time  which is better than all preceding ones. Then this strategy, called 1/e-strategy, has the following properties:
which is better than all preceding ones. Then this strategy, called 1/e-strategy, has the following properties:
The 1/e-strategy
- (i) yields for all
 a success probability of at least 1/e,
a success probability of at least 1/e,
- (ii) is the unique strategy guaranteeing this lower success probability bound 1/e, and the bound is optimal,
- (iii) selects, if there is at least one applicant, none at all with probability exactly 1/e.
When the 1/e-law was discovered in 1984 it came as a surprise. The reason was that a value of about 1/e had been considered before as being out of reach in a model for unknown  , whereas now this value was achieved as a lower bound, and this in a model with arguably weaker hypotheses (see e.g. Math. Reviews 85:m).
, whereas now this value was achieved as a lower bound, and this in a model with arguably weaker hypotheses (see e.g. Math. Reviews 85:m).
This law is sometimes confused with the solution for the secretary problem because of the similar role of the number 1/e. Note however, that in the 1/e-law, this role is stronger and more general. The result is also stronger, since it holds for an unknown number of applicants and since the model is more tractable for applications.
The Game of Googol
According to Ferguson 1989 the Secretary Problem appeared for the first time in print in Martin Gardner's column of Scientific American in 1960. Here is how Martin Gardner formulated the problem: "Ask someone to take as many slips of paper as he pleases, and on each slip write a different positive number. The numbers may range from small fractions of 1 to a number the size of a googol (1 followed by a hundred 0s) or even larger. These slips are turned face down and shuffled over the top of a table. One at a time you turn the slips face up. The aim is to stop turning when you come to the number that; you guess to be the largest of the series. You cannot go back and pick a previously turned slip. If you turn over all the slips, then of course you must pick the last one turned."
In the paper "Who solved the Secretary problem?" Ferguson 1989 pointed out that the Secretary Problem remained unsolved as it was stated by M. Gardner, that is as a two-person zero-sum game with two antagonistic players. In this game Alice, the informed player, writes secretly distinct numbers on  cards. Bob, the stopping player, observes the actual values and can stop turning cards whenever he wants, winning if the last card turned has the overall maximum number. The difference with the basic Secretary Problem is that Bob observes the actual values written on the cards which he can use in his decision procedures. The numbers on cards are analogous to the numerical qualities of applicants in some versions of the Secretary Problem. The joint probability distribution of the numbers is under the control of Alice.
cards. Bob, the stopping player, observes the actual values and can stop turning cards whenever he wants, winning if the last card turned has the overall maximum number. The difference with the basic Secretary Problem is that Bob observes the actual values written on the cards which he can use in his decision procedures. The numbers on cards are analogous to the numerical qualities of applicants in some versions of the Secretary Problem. The joint probability distribution of the numbers is under the control of Alice.
Bob wants to guess the maximum number with highest possible probability, while Alice' goal it to keep this probability as low as possible. It is not optimal for Alice to sample the numbers independently from some fixed distribution, and she can play better by choosing random numbers in some dependent way. For 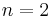 Alice has no minimax strategy, which is closely related to a paradox of T. Cover. But for
Alice has no minimax strategy, which is closely related to a paradox of T. Cover. But for 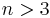 the game has a solution: Alice can choose random numbers (which are dependent random variables) in such a way that Bob cannot play better than using the classical stopping strategy based on the relative ranks (Gnedin 1994).
the game has a solution: Alice can choose random numbers (which are dependent random variables) in such a way that Bob cannot play better than using the classical stopping strategy based on the relative ranks (Gnedin 1994).
Heuristic performance
The remainder of the article deals again with the secretary problem for a known number of applicants.
Stein, Seale & Rapoport 2003 derived the expected success probabilities for several psychologically plausible heuristics that might be employed in the secretary problem. The heuristics they examined were:
- The cutoff rule (CR): Do not accept any of the first y applicants; thereafter, select the first encountered candidate (i.e., an applicant with relative rank 1). This rule has as a special case the optimal policy for the CSP for which y = r.
- Candidate count rule (CCR): Select the y encountered candidate. Note, that this rule does not necessarily skip any applicants; it only considers how many candidates have been observed, not how deep the decision maker is in the applicant sequence.
- Successive non-candidate rule (SNCR): Select the first encountered candidate after observing y non-candidates (i.e., applicants with relative rank > 1).
Note that each heuristic has a single parameter y. The figure (shown on right) displays the expected success probabilities for each heuristic as a function of y for problems with n = 80.
Cardinal payoff variant
Finding the single best applicant might seem like a rather strict objective. One can imagine that the interviewer would rather hire a higher-valued applicant than a lower-valued one, and not only be concerned with getting the best. That is, he will derive some value from selecting an applicant that is not necessarily the best, and the value he derives is increasing in the value of the one he selects.
To model this problem, suppose that the  applicants have "true" values that are random variables X drawn i.i.d. from a uniform distribution on [0, 1]. Similar to the classical problem described above, the interviewer only observes whether each applicant is the best so far (a candidate), must accept or reject each on the spot, and must accept the last one if he is reached. (To be clear, the interviewer does not learn the actual relative rank of each applicant. He learns only whether the applicant has relative rank 1.) However, in this version his payoff is given by the true value of the selected applicant. For example, if he selects an applicant whose true value is 0.8, then he will earn 0.8. The interviewer's objective is to maximize the expected value of the selected applicant.
applicants have "true" values that are random variables X drawn i.i.d. from a uniform distribution on [0, 1]. Similar to the classical problem described above, the interviewer only observes whether each applicant is the best so far (a candidate), must accept or reject each on the spot, and must accept the last one if he is reached. (To be clear, the interviewer does not learn the actual relative rank of each applicant. He learns only whether the applicant has relative rank 1.) However, in this version his payoff is given by the true value of the selected applicant. For example, if he selects an applicant whose true value is 0.8, then he will earn 0.8. The interviewer's objective is to maximize the expected value of the selected applicant.
Since the applicant's values are i.i.d. draws from a uniform distribution on [0, 1], the expected value of the tth applicant given that 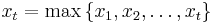 is given by
is given by
As in the classical problem, the optimal policy is given by a threshold, which for this problem we will denote by  , at which the interviewer should begin accepting candidates. Bearden 2006 showed that c is either
, at which the interviewer should begin accepting candidates. Bearden 2006 showed that c is either 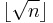 or
or 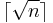 . (In fact, whichever is closest to
. (In fact, whichever is closest to 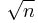 .) This follows from the fact that given a problem with
.) This follows from the fact that given a problem with  applicants, the expected payoff for some arbitrary threshold 1 = c = n is
applicants, the expected payoff for some arbitrary threshold 1 = c = n is
Differentiating 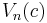 with respect to c, one gets
with respect to c, one gets
Since 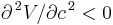 for all permissible values of
for all permissible values of  , we find that
, we find that  is maximized at
is maximized at 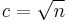 . Since V is convex in
. Since V is convex in  , the optimal integer-valued threshold must be either
, the optimal integer-valued threshold must be either 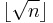 or
or 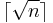 . Thus, for most values of
. Thus, for most values of  the interviewer will begin accepting applicants sooner in the cardinal payoff version than in the classical version where the objective is to select the single best applicant. Note that this is not an asymptotic result: It holds for all
the interviewer will begin accepting applicants sooner in the cardinal payoff version than in the classical version where the objective is to select the single best applicant. Note that this is not an asymptotic result: It holds for all  .
.
Experimental studies
Psychologists and experimental economists have studied the decision behavior of actual people in secretary problems.[1] In large part, this work has shown that people tend to stop searching too soon. This may be explained, at least in part, by the cost of evaluating candidates. Extrapolating to real world settings, this might suggest that people do not search enough whenever they are faced with problems where the decision alternatives are encountered sequentially. For example, when trying to decide at which gas station to stop for gas, people might not search enough before stopping. If true, then they would tend to pay more for gas than they might had they searched longer. The same may be true when people search online for airline tickets, say. Experimental research on problems such as the secretary problem is sometimes referred to as behavioral operations research.
Origin of the problem
The secretary problem was apparently introduced in 1949 by Merrill M. Flood, who called it the fiancée problem in a lecture he gave that year. He referred to it several times during the 1950s, for example in a conference talk at Purdue on 9 May 1958, and it eventually became widely known in the folklore although nothing was published at the time. In 1958 he sent a letter to Leonard Gilman, with copies to a dozen friends including S. Karlin and J. Robbins, outlining a proof of the optimum strategy, with an appendix by R. Palermo who proved that all strategies are dominated by a strategy of the form "reject the first p unconditionally, then accept the next candidate". (See Flood (1958).)
The first publication was apparently by Martin Gardner in Scientific American, February 1960. He had heard about it from John H. Fox, Jr., and L. Gerald Marnie, who had independently come up with an equivalent problem in 1958; they called it the "game of Googol". Fox and Marnie did not know the optimum solution; Gardner asked for advice from Leo Moser, who (together with J. R. Pounder) provided a correct analysis for publication in the magazine. Soon afterwards, several mathematicians wrote to Gardner to tell him about the equivalent problem they had heard via the grapevine, all of which can most likely be traced to Flood's original work.
The 1/e-law is due to F. Thomas Bruss (1984)
A 1989 paper by T. S. Ferguson has an extensive bibliography, and points out that a similar (but different) problem had been considered by Arthur Cayley in 1875 and even by Johannes Kepler long before that.
See also
References
- Bearden, J.N. (2006). "A new secretary problem with rank-based selection and cardinal payoffs". Journal of Mathematical Psychology 50: 58–9. doi:10.1016/j.jmp.2005.11.003.
- Bearden, J.N., Murphy, R.O. Rapoport, A. (2005). "A multi-attribute extension of the secretary problem: Theory and experiments". Journal of Mathematical Psychology 49 (5): 410–425. doi:10.1016/j.jmp.2005.08.002.
- Bearden, J.N., Rapoport, A., Murphy R.O. (2006). "Sequential observation and selection with rank-dependent payoffs: An experimental test". Management Science 52 (9): 1437–49. doi:10.1287/mnsc.1060.0535.
- F. Thomas Bruss (1984). "A unified Approach to a Class of Best Choice problems with an Unknown Number of Options". Annals of Probability 12 (3): 882–891. doi:10.1214/aop/1176993237.
- F. Thomas Bruss (2000). "Sum the odds to one and stop". Annals of Probability 28 (3): 1384–91. doi:10.1214/aop/1019160340.
- Ferguson, T.S.[2] (1989). "Who solved the secretary problem?". Statistical science 4 (3): 282–296. doi:10.1214/ss/1177012493.
- Gnedin, A. (1994). "A solution to the game of Googol". Annals of Probability 22 (3): 1588–1595. doi:10.1214/aop/1176988613.
- Freeman, P.R. (1983). "The secretary problem and its extensions: A review". International Statistical Review / Revue Internationale de Statistique 51 (2): 189–206. doi:10.2307/1402748. JSTOR 1402748.
- Hill, T.P. "Knowing When to Stop". American Scientist, Vol. 97, 126-133 (2009). (For French translation, see cover story in the July issue of Pour la Science (2009))
- Seale, D.A., Rapoport, A. (1997). "Sequential decision making with relative ranks: An experimental investigation of the 'secretary problem'". Organizational Behavior and Human Decision Processes 69 (3): 221–236. doi:10.1006/obhd.1997.2683.
- Stein, W.E.; Seale, D.A.; Rapoport, A. (2003). "Analysis of heuristic solutions to the best choice problem". European Journal of Operational Research 151: 140–152. doi:10.1016/S0377-2217(02)00601-X.
- Merrill R. Flood, letter written in 1958, a copy of which can be found in the Martin Gardner papers at Stanford University Archives, series 1, box 5, folder 19.
- Martin Gardner, New Mathematical Diversions from Scientific American. Simon and Schuster, 1966, Chapter 3, Problem 3 [reprints his original column published in February 1960 with additional comments].
- Miller, Geoffrey F. (2001). The mating mind: how sexual choice shaped the evolution of human nature. Anchor Books. ISBN 0-385-49517-X.
- Framing Our Thoughts: Ecological Rationality as Evolutionary Psychology's Answer to the Frame Problem, Timothy Ketelaar and Peter M. Todd, Chapter 5 of Conceptual Challenges in Evolutionary Psychology, p. 187.
- Sardelis, D., Valahas, T. (March 1992). "Decision Making: A Golden Rule". American Mathematical Monthly 99 (3): 935–942.
Notes
- ^ Bearden, Murphy, and Rapoport, 2006; Bearden, Rapoport, and Murphy, 2006; Seale and Rapoport, 1997
- ^ A mathematics professor at UCLA and the father of Chris "Jesus" Ferguson, the professional poker player

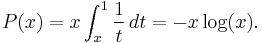
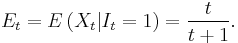
![V_{n}(c)=\sum_{t=c}^{n-1}\left[\prod_{s=c}^{t-1}\left(\frac{s-1}{s}\right)\right]\left(\frac{1}{t%2B1}\right)
%2B\left[\prod_{s=c}^{n-1}\left(\frac{s-1}{s}\right)\right]\frac{1}{2}={\frac {2cn-{c}^{2}%2Bc-n}{2cn}}.](/2012-wikipedia_en_all_nopic_01_2012/I/c854aae43537082746b2f028c33a7999.png)